Binary Search Tree(이진 탐색 트리)

- 모든 노드가 자신의 왼쪽 서브트리에는 현재노드보다 작은 키값이, 오른쪽 서브트리에는 현재 노드보다 큰 값이 오는 규칙을 만족하는 이진트리
- 모든 왼쪽 자식들 <= n < 모든 오른쪽 자식들 (모든 노드 n에 대해서 반드시 참)
- 이진 탐색 트리는 이진 탐색을 쉽게 할 수 있도록 만들어진 트리
- 이진 탐색 트리의 조건
- 이진 탐색 트리의 노드에 저장된 키는 유일하다.
- 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다.
- 루트 노드의 키가 오른쪽 서브트리를 구성하는 어떠한 노드의 키보다 작다.
- 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.
- 이진 탐색트리의 탐색 연산은 평균 O(log n)의 시간 복잡도를 갖는다.
- 비교적 삽입, 삭제가 효율적인 자료구조이다.
- 이진 탐색 트리는 Skewed Tree(편향 트리)가 될 수 있다.
- 저장 순서에 따라 계속 한 쪽으로만 노드가 추가되는 경우가 발생하기 때문이다.
- 이를 해결하기 위해 균형잡힌 이진 탐색 트리를 고안. 대표적인 것은 Red-Black Tree(레드블랙트리)와 AVL트리다.
이진 탐색 트리의 연산
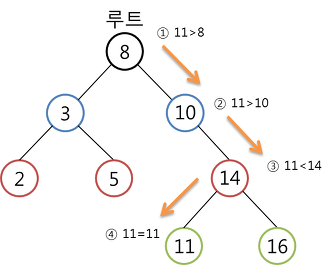
탐색 연산
- 탐색은 항상 루트 노드에서 시작한다.
- 먼저, 키값 x와 루트 노드의 키값을 비교한다.
- if (x == 루트) 원하는 원소를 찾았으므로 탐색 성공
- else if (루트 > x) 루트의 왼쪽 서브트리에 대해서 탐색 연산 수행
- else if (루트 < x) 루트의 오른쪽 서브트리에 대해서 탐색 연산 수행

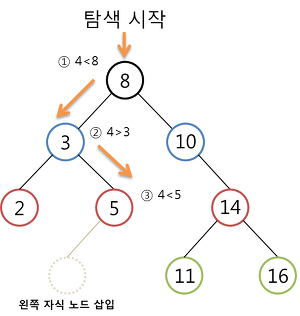
삽입 연산
- 원소를 삽입하려면 먼저 이진 탐색 트리에 같은 원소가 있는지를 확인하기 위해 탐색을 해야한다.
- if (탐색 성공) 이미 같은 원소가 트리 내에 있는 것이므로 삽입 연산을 수행하지 않는다.
- else if (탐색 실패) 크기를 비교하여 찾아간 노드의 위치에 같은 원소가 없는 것이므로 그 자리에 원소를 삽입

삭제 연산
- 원소를 삭제하는 경우 자식 노드의 수에 따라 세 가지 경우가 있다.
- 노드를 삭제한 후에도 여전히 이진 탐색트리를 유지해야 하기 때문에 각각의 경우에 따라 후속 처리가 필요하다.
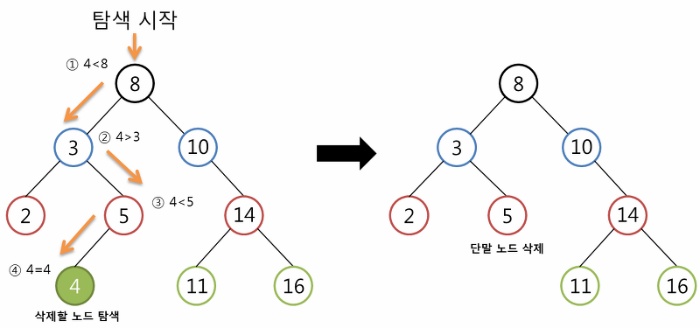
① 삭제할 노드가 단말 노드인 경우
- 노드를 삭제하고, 부모노드의 링크 필드를 null로 설정하는 작업으로 간단히 처리할 수 있다.

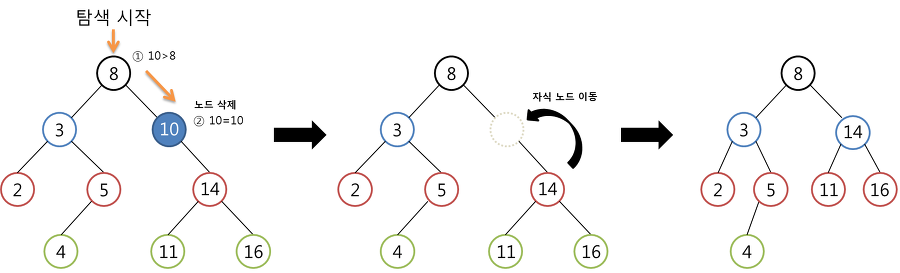
② 삭제할 노드가 한 개의 자식노드를 가진 경우 (차수가 1인 경우)
- 노드를 삭제하고 나면 자식 노드가 트리에서 떨어져서 고아가 되어버린다.
- 남겨진 자식노드를 삭제한 부모노드의 자리로 올려준다.
- 자식이 부모의 유산을 물려받듯이 자식노드가 부모노드의 자리를 물려받는다.

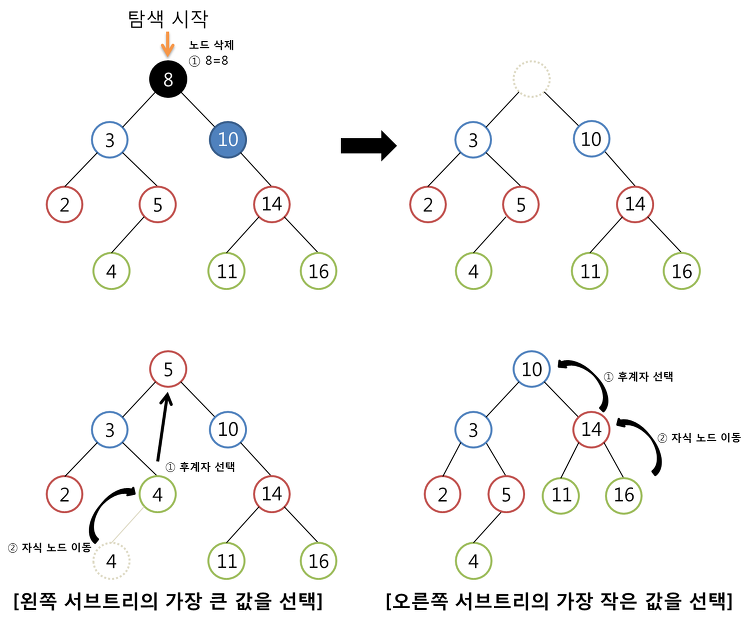
③ 삭제할 노드가 두 개의 자식노드를 가진 경우 (차수가 2인 경우)
- 노드를 삭제하고 나면 부모노드의 자리를 자식노드에게 물려줄 때 왼쪽, 오른쪽 중 어느쪽에 물려줄 지 생각해야한다.
- 이진탐색 트리의 특성에 따라서 삭제할 노드의 자리에 위치할 값은 왼쪽 서브 트리에 있는 노드들의 값보다 커야하고, 오른쪽 서브 트리에 있는 노드들의 키값보다는 작아야한다.
- 그러므로 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 자손 노드 또는 오른쪽 서브 트리에서 가장 작은 자손 노드가 삭제할 노드의 자리에 올 수 있다.

이진 탐색 트리의 자바를 활용한 구현
TreeNode.java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class TreeNode {
char data;
TreeNode left;
TreeNode right;
public TreeNode(){
this.left = null;
this.right = null;
}
public TreeNode(char data){
this.data = data;
this.left = null;
this.right = null;
}
public Object getData(){
return data;
}
}
BinarySearchTree.java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class BinarySearchTree {
private TreeNode root = new TreeNode();
public TreeNode insertKey(TreeNode root, char x) {
TreeNode p = root;
TreeNode newNode = new TreeNode(x);
if(p==null){
return newNode;
}else if(p.data>newNode.data){
p.left = insertKey(p.left, x);
return p;
}else if(p.data<newNode.data){
p.right = insertKey(p.right, x);
return p;
}else{
return p;
}
}
public void insertBST(char x){
root = insertKey(root, x);
}
public TreeNode searchBST(char x){
TreeNode p = root;
while(p!=null){
if(x<p.data) p = p.left;
else if(x>p.data) p = p.right;
else return p;
}
return p;
}
public void inorder(TreeNode root){
if(root!=null){
inorder(root.left);
System.out.print(root.data + " ");
inorder(root.right);
}
}
public void printBST(){
inorder(root);
System.out.println();
}
}
Main.java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Test {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
bst.insertBST('G');
bst.insertBST('I');
bst.insertBST('H');
bst.insertBST('D');
bst.insertBST('B');
bst.insertBST('M');
bst.insertBST('N');
bst.insertBST('A');
bst.insertBST('J');
bst.insertBST('E');
bst.insertBST('Q');
System.out.println("Binary Tree >>>");
bst.printBST();
System.out.println("Is There \"A\" ? >>> ");
TreeNode p1 = bst.searchBST('A');
if(p1!=null){
System.out.println(p1.data + " 탐색 성공");
}else{
System.out.println("탐색 실패");
}
System.out.println("Is There \"Z\" ? >>> ");
TreeNode p2 = bst.searchBST('Z');
if(p2!=null){
System.out.println(p2.data + " 탐색 성공");
}else{
System.out.println("탐색 실패");
}
}
}